Quantum circuits
Circuit model is a sequence of some building blocks that carry out our computations, called gates 
Single qubit gates
-
classical example: NOT
-
quantum example: as quantum theory is unitary, quantum gates are represented by unitary matrices: $u_+ u = \vec I$
direct notation: \(\begin{pmatrix} u_{00} & u_{01} \\ u_{10} & u_{11} \end{pmatrix} = u_{00} \vert 0 \rangle \langle 0 \vert + u_{01}\vert 0 \rangle \langle 1 \vert + u_{10}\vert 1 \rangle \langle 0 \vert + u_{11}\vert 1 \rangle \langle 1 \vert\)
-
\[\sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} = \vert 0 \rangle \langle 1 \vert + \vert 1 \rangle \langle 0 \vert\]
\[\sigma_x \vert 0 \rangle =
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
\cdot
\begin{pmatrix} 1 \\ 0 \end{pmatrix} =
\begin{pmatrix} 0 \\ 1 \end{pmatrix} =
\vert 1 \rangle\]
\[\sigma_x \vert 1 \rangle =
(
\vert 0 \rangle \langle 1 \vert +
\vert 1 \rangle \langle 0 \vert
)
\cdot \vert 1 \rangle =
\vert 0 \rangle \langle 1 \vert 1 \rangle +
\vert 1 \rangle \langle 0 \vert 1 \rangle =
\vert 0 \rangle\]
=> bit flip $\cong$ NOT-gate. e.g.
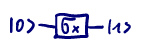 => rotation around the X axis by $\pi$.
=> rotation around the X axis by $\pi$. -
\[\sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \vert 0 \rangle \langle 0 \vert - \vert 1 \rangle \langle 1 \vert\]
\[\sigma_z \vert + \rangle =
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
\cdot \frac{1}{\sqrt{2}}
\begin{pmatrix} 1 \\ 1 \end{pmatrix} =
\frac{1}{\sqrt{2}}
\begin{pmatrix} 1 \\ -1 \end{pmatrix} =
\vert - \rangle\]
\[\sigma_z \vert - \rangle =
(
\vert 0 \rangle \langle 0 \vert -
\vert 1 \rangle \langle 1 \vert
)
\cdot \frac{1}{\sqrt{2}}
(
\vert 0 \rangle - \vert 1 \rangle
) =
\frac{1}{\sqrt{2}}
(
\vert 0 \rangle + \vert 1 \rangle
) =
\vert + \rangle\]
=> phase flip => rotation around $z\cdot$axis by $\pi$
-
\(\sigma_y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} = i \cdot \sigma_z \cdot \sigma_x\) => bit & phase flip
-
$\sigma_x, \sigma_y, \sigma_z$ are the so-called Poly matrices \({\sigma_i}^2 = \vec I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\) (dose nothing)
together with identify $\vec I$ they form a basis of 2x2 matrices.
any 1-qubit rotation can be written as linear combination of them.
-
Hadamard gate:
\[H = \frac{1} {\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} =- \frac{1} {\sqrt{2}} ( \vert 0 \rangle \langle 0 \vert + \vert 0 \rangle \langle 1 \vert + \vert 1 \rangle \langle 0 \vert - \vert 1 \rangle \langle 1 \vert )\] \[H \vert 0 \rangle = \frac{1} {\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{1} {\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \vert + \rangle\] \[H \vert 1 \rangle = ( \vert 0 \rangle \langle 0 \vert + \vert 0 \rangle \langle 1 \vert + \vert 1 \rangle \langle 0 \vert - \vert 1 \rangle \langle 1 \vert ) \cdot \vert 1 \rangle = \frac{1}{\sqrt{2}} ( \vert 0 \rangle - \vert 1 \rangle ) = \vert - \rangle\]H can user for creates superposition -> $H\vert + \rangle = \vert 0 \rangle , H \vert - \rangle = \vert 1 \rangle$ => used to change between X & Z basis.
-
similary, as \(S = \begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix}\) adds $90^{\circ}$ to the phase $\varphi$: $S\cdot \vert + \rangle = \vert +i \rangle, S \vert - \rangle = \vert -i \rangle$
=> used to change between X & Y basis,
- $S \cdot H$ is applied to change Z to Y basis.
Multi patent quantum states
-
we use these products to describe multi patent states: $\vert a \rangle \otimes \vert b \rangle = $ \(\begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \otimes \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} a_1 b_1 \\ a_1 b_2 \\ a_2 b_1 \\ a_2 b_2 \end{pmatrix}\)
-
example: system A is in state ${\vert 1 \rangle}_A$ and system B is in the state ${\vert 0 \rangle}_B$
=> the total(bipartite) state is ${\vert 1 0 \rangle}_{AB} := {\vert 1 \rangle}_A \otimes {\vert 0 \rangle}_B = $ \(\begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}\)
=> remark: states of this form are called uncorrelated(不相关), but there are alse states that cannot be written as ${\vert \psi \rangle}_A \otimes {\vert \varphi \rangle}_B$. These states are correlated() and sometimes even entangled(very strong corrlation) e.g.
\({ {\vert \phi \rangle}^{(00)}}_{AB} = \frac{1}{\sqrt{2}} ( {\vert 00 \rangle}_{AB} + {\vert 11 \rangle}_{AB} ) = \frac{1}{\sqrt{2}} ( \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} ) = \frac{1}{\sqrt{2}} ( \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} )= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \end{pmatrix}\) a so-called Bell state, used for teleportation, cryptography, etc.
Two-qubit gates
-
classical exampl: XOR
 -> irreversible (-> given the output we cannot recover the input)
-> irreversible (-> given the output we cannot recover the input)BUT: as quantum theory is unitary, we only consider unitary gate and there are always reversible. $u^+ u = \vec{I} \Leftrightarrow u^{-1} = u^+$
-
quantum example:
CNOT = \(\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} = \vert 00 \rangle \langle 00 \vert + \vert 01 \rangle \langle 01 \vert + \vert 10 \rangle \langle 11 \vert + \vert 11 \rangle \langle 10 \vert +\) => $CNOT \cdot \vert 00 \rangle = $ \(CNOT \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = {\vert 00 \rangle}_{xy}, \quad CNOT{\vert 10 \rangle}_{xy} = {\vert 11 \rangle}_{xy}\)
input output x y x $x \otimes y$ 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 0 => circuit:
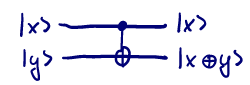 (reversible XOR)
(reversible XOR)=> we can show that evet function f can described by a reversible circuit
=> quantum circuits can perform all function that can be calculated classically.