Qubits and quantum states
Form bits to qubits
-
classical states for computation are either “0” or “1”
-
in quantum mechaincs, a state can be in superposition (simultaneously in zero and one)
-> superposition allow to perform calcuation on many states at the same time.
-> quantum algorithms with exponentially speed up.
But: once we measure the superposition state, it collapse to one of its states (we can only get one “answber” and not all answer to all states in the superposition)
-> it is not that easy to design quantum algorithmsm, but we can use interference effects (“wrong answers” cancled each other out, while the “right answer” remains)
Dirac notation(狄拉克符号)
-
used to describe quantum states
-
ket: \(\vert a \rangle = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\)
-
bra: \(\langle b \vert = {\vert b \rangle}^+ = {\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}}^+ = \begin{pmatrix} b_1^* & b_2^* \end{pmatrix}\)
-
bra-ket: \(\langle b \vert a \rangle = a_1 b_1^* + a_2 b_2^* = {\langle a \vert b \rangle}^*\)
-
ket-bra: \(\vert a \rangle \langle b \vert = \begin{pmatrix} a_1 b_1^* & a_1 b_2^* \\ a_2 b_1^* & a_2 b_2^* \end{pmatrix}\)
-
-
we define the states \(\vert 0 \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} and \vert 1 \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\) , which are orthogonal(正交) ( \(\langle 0 \vert 1 \rangle = \begin{pmatrix} 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = 1 \cdot 0 + 0 \cdot 1 = 0\) )
-
all quantum states are normalizedm(归一) i.e. , $\langle \psi \vert \psi \rangle=1$, eg. \(\vert \psi \rangle=\frac{1}{\sqrt 2}\cdot(\vert 0 \rangle + \vert 1 \rangle)=\begin{pmatrix}\frac{1}{\sqrt 2} \\ \frac{1}{\sqrt 2} \end{pmatrix}\)
Measurement
-
we choose orthogonal bases to descrive and measure aquantum states
-
during a measurement onto the basis {$\vert 0 \rangle, \vert 1 \rangle$}, the state will collapse into either state $\vert 0 \rangle$ or $\vert 1 \rangle$ => as those are the eigenstates of the $\sigma_z$, we call this a Z-measurement
-
there are infinitely many different basism, but other common ones are {$\vert + \rangle := \frac{1}{\sqrt 2}\cdot(\vert 0 \rangle + \vert 1 \rangle), \vert - \rangle := \frac{1}{\sqrt 2}\cdot(\vert 0 \rangle - \vert 1 \rangle)$} and {$\vert +i \rangle := \frac{1}{\sqrt 2}\cdot(\vert 0 \rangle + i\vert 1 \rangle), \vert -i \rangle := \frac{1}{\sqrt 2}\cdot(\vert 0 \rangle - i\vert 1 \rangle)$} correspond to eigenstates of $\sigma_x$ and $\sigma_y$, respectively
-
Born rule: the probobility that a state $\vert \psi \rangle$ collapse during a projective measurement onto the basis {$\vert x \rangle$, $\vert x^+ \rangle$}, to the state $\vert x \rangle$ is given by $P(x) = {|\langle x \vert \psi \rangle |}^2, \sum{P(x)} = 1$
-
examples:
-
$\vert \psi \rangle = 1 / {\sqrt 3} (\vert 0 \rangle + {\sqrt 2} \vert 1 \rangle)$ is measuemnt in the basis {$\vert 0 \rangle$, $\vert 1 \rangle$}:
-> $P(0) = {|\langle0 \vert \frac{1}{\sqrt 3}(\vert 0\rangle+{\sqrt 2}\vert 1 \rangle)|}^2 = {|\frac{1}{\sqrt 3}\langle 0 \vert 0 \rangle + \sqrt \frac{2}{3}\langle 0 \vert 1 \rangle |}^2 = \frac{1}{3}$
-> $P(1) = 2/3$
-
$\vert \psi \rangle = 1/2( \vert 0 \rangle - \vert 1 \rangle )$ is measuemnt in the basis {$\vert + \rangle , \vert - \rangle$} :
-> $P(+) = {| \langle + \vert \psi \rangle |}^2 = {|\frac{1}{\sqrt 2}(\langle 0 \vert + \langle 1 \vert ) \cdot \frac {1}{\sqrt 2} \cdot ( \vert 0 \rangle - \vert 1 \rangle )|}^2 = 0$
-
Bloch sphere(布洛赫球面)
We can write any normalized(pure) quantum state as $\vert \psi \rangle = cos{\frac{\theta}{2}}\vert 0 \rangle + e^{i\varphi}\sin{\frac{\theta}{2}} \vert 1 \rangle$, where $\varphi \in [0, 2\pi]$ describe the relative phase and $\theta \in [0, \pi]$ determines the probobility to measure $\vert 0 \rangle / \vert 1 \rangle$: $P(\vert 0 \rangle) = {cos{\frac{\theta}{2}}}^2, P(\vert 1 \rangle) = {\sin{\frac{\theta}{2}}}^2$
=> all normalized pure states can be illustrated on the surface of a sphere with radius $\vert \vec r \vert = 1$, which we call the Bloch sphere
=> the coordinates of such a state are given by the Bloch vector:
\[\vec r = \begin{pmatrix} \sin{\theta} \cos{\varphi} \\ \sin{\theta} \sin{\varphi} \\ \cos{\theta} \end{pmatrix}\]examples:
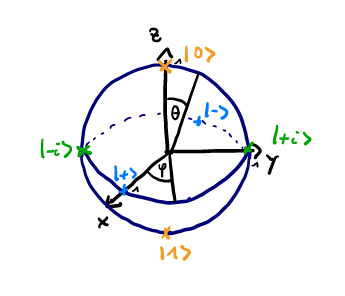
- $\vert 0 \rangle: \quad \theta = 0, \varphi \quad arbi \rightarrow$ \(\vec r = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)
- $\vert 1 \rangle: \quad \theta = \pi, \varphi \quad arbi \rightarrow$ \(\vec r = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\)
- $\vert + \rangle: \quad \theta = \frac{\pi}{2}, \varphi = 0 \rightarrow$ \(\vec r = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\)
- $\vert - \rangle: \quad \theta = \frac{\pi}{2}, \varphi = \pi \rightarrow$ \(\vec r = \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}\)
- $\vert +i \rangle: \quad \theta = \frac{\pi}{2}, \varphi = \frac{\pi}{2} \rightarrow$ \(\vec r = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\)
- $\vert -i \rangle: \quad \theta = \frac{\pi}{2}, \varphi = \frac{3\pi}{2} \rightarrow$ \(\vec r = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)
References
Qiskit lecture Note: Qubits and Quantum States, Quantum Circuits, Measurements